We've completed our first experiment, and established the framework for our algorithm, which boils down to computing the following probability:
So far we have just used an unigram model based on color histograms to determine these probabilities. We want to add bigram model for spatial relationships between segments. In addition, we also want to incorporate a parse grammar of objects that models contextual relationships between segments.
We will need to assign weights to each model so that the total probability adds up to 1. We are still researching exactly how to learn what these ideal weights should be, we are hoping something like a CRF model will do the trick, or we can just play around with different values. Here's one potential example:
Feature Unigram Bigram
Color 0.2 0
Centroid 0 0.2
Area 0.05 0.2
Context 0.15 0.2
For contextual relationships, we intend to use a parse grammar similar to the one described here
For ours, we would use segments instead of lines as the elements of the grammar. Ideally, we would like our grammar to represent the 3D geometry of the scene (as in the link above), but to start we will probably just identify some basic labels:
So far we have just used an unigram model based on color histograms to determine these probabilities. We want to add bigram model for spatial relationships between segments. In addition, we also want to incorporate a parse grammar of objects that models contextual relationships between segments.
We will need to assign weights to each model so that the total probability adds up to 1. We are still researching exactly how to learn what these ideal weights should be, we are hoping something like a CRF model will do the trick, or we can just play around with different values. Here's one potential example:
Feature Unigram Bigram
Color 0.2 0
Centroid 0 0.2
Area 0.05 0.2
Context 0.15 0.2
For contextual relationships, we intend to use a parse grammar similar to the one described here
For ours, we would use segments instead of lines as the elements of the grammar. Ideally, we would like our grammar to represent the 3D geometry of the scene (as in the link above), but to start we will probably just identify some basic labels:
Foreground Background
/ \ / | \
table chair wall ceiling floor
/ \ / \ / \ \
legs top legs top door window carpet
Training data - need to figure this out
1) We can create our own training data from simple indoor scenes. For each image, we will have a manually segmented image for each level in the parse tree
If we construct our own data, how many images will we need for our training data?
2) Find something online? We're not sure if anything like what we've described exists.
How to split and merge clusters? (some ideas)
Ideally, we want our algorithm to "find" new objects in the scene, based on its current understanding of the scene. This involves increasing or decreasing the number of segments at each iteration, eventually converging to the proper amount.
For example, given clusters A-G, and labels table and chair. Let's say we know with high probability that cluster A is label 'table', and further we know from contextual relationships that if we see label 'table', then we should see label 'chair' nearby.
If none of the nearby clusters correspond to a chair, (that is, the probability of P(B or C or D or E or F or G = 'chair' | A = 'table') is really low), then we split one of the clusters (increase k), to try to find a cluster with label 'chair'. Ideally, we want to split the cluster that we have the lowest confidence in its labels.
We split the cluster where we expect the part/object to be (using computer vision techniques, we know generally where it should be).
We merge clusters when they are empty, really small.
legs top legs top door window carpet
Training data - need to figure this out
1) We can create our own training data from simple indoor scenes. For each image, we will have a manually segmented image for each level in the parse tree
If we construct our own data, how many images will we need for our training data?
2) Find something online? We're not sure if anything like what we've described exists.
How to split and merge clusters? (some ideas)
Ideally, we want our algorithm to "find" new objects in the scene, based on its current understanding of the scene. This involves increasing or decreasing the number of segments at each iteration, eventually converging to the proper amount.
For example, given clusters A-G, and labels table and chair. Let's say we know with high probability that cluster A is label 'table', and further we know from contextual relationships that if we see label 'table', then we should see label 'chair' nearby.
If none of the nearby clusters correspond to a chair, (that is, the probability of P(B or C or D or E or F or G = 'chair' | A = 'table') is really low), then we split one of the clusters (increase k), to try to find a cluster with label 'chair'. Ideally, we want to split the cluster that we have the lowest confidence in its labels.
We split the cluster where we expect the part/object to be (using computer vision techniques, we know generally where it should be).
We merge clusters when they are empty, really small.







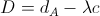.gif)
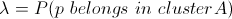
.gif)
(strawberries_fullcolor).tif)